本文首先对Sim2real问题作出了简要介绍，并简单对其方法作出分类。接着，对于其中的domain randomization方法给出bilevel optimization的形式，最后调研了基于上述优化形式（或类似形式）下的优化问题求解方案。

此外 Lilian Weng (Open AI) 的博客 对 DR 问题做了深入探讨，极具价值。

概述

sim2real的全称是simulation to reality，是强化学习的一个分支，同时也属于transfer learning的一种。主要解决的问题是机器人领域中，直接让机器人或者机械臂在现实环境中与环境进行交互、采样时，会出现以下两个比较严重的问题：

• 采样效率太低（在用强化学习算法解决机器人相关问题时，所需要的样本量一般会达到上千万，在现实环境中采集如此数量级的样本要耗费几个月的时间）
• 安全问题 （由于强化学习需要通过智能体在环境中进行大范围的随机采样来进行试错，因而在某些时刻其做出的行为可能会损伤机器人自身，例如手臂转动角度过大或者避障任务中由于碰撞造成的不可逆损伤等等；也可能会损害周围的环境甚至生物）

但是如果我们在模拟器中进行强化学习算法的训练，以上两个问题均可迎刃而解。但是，这里同样会存在一个问题，由于模拟器对于物理环境的建模都是存在误差的，因而在模拟环境中学习到的最优策略是否可以直接在现实环境中应用呢？答案往往是否定的，我们把这个问题称为 “reality gap”。而sim2real的工作就是去尝试解决这个问题。

这里值得注意的一点是，虽然这个方向叫做sim2real，其实其中的所有的算法都可以直接应用在sim2sim，real2real等的任务中。

[引自：https://zhuanlan.zhihu.com/p/106216904]

本文找了一篇survey，对其中的内容作出整理，意图对整个sim2real领域有一个大致的了解。

1. Sim2real 分类

在下述工作中，Sim2real被分为了以下4个类别

W. Zhao, J. P. Queralta and T. Westerlund, “Sim-to-Real Transfer in Deep Reinforcement Learning for Robotics: a Survey,” 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, ACT, Australia, 2020, pp. 737-744, doi: 10.1109/SSCI47803.2020.9308468.

tax1.1 Zero-shot Transfer

建立一个逼真的模拟器，或者有足够的模拟经验，这样模型就可以直接应用到现实环境中。这种策略通常称为zero-shot transfer或direct transfer。建立真实世界精确模型的系统识别（System Identification）和域随机化（Domain Randomization Methods）是可以被视为一次性迁移的技术。我们在第 III-B 节和第III-C节中分别讨论了这两个问题。

tax1.2 System Identification

值得注意的是，模拟器不是真实世界的忠实代表。系统识别[51]正是为了建立物理系统的精确数学模型，并使模拟器更真实，需要仔细校准。尽管如此，获得足够逼真的模拟器的挑战仍然存在。例如，很难构建高质量的渲染图像来模拟真实的视觉。此外，同一机器人的许多物理参数可能会因温度、湿度、定位或其磨损而发生显著变化，这给系统识别带来了更大的困难。

tax1.3 Domain Randomization Methods

领域随机化是这样一种想法[52]，我们可以高度随机化模拟，而不是仔细建模真实世界的所有参数，以覆盖真实世界数据的真实分布，尽管模型和真实世界之间存在偏差。图3a显示了域随机化的范例。

tax1.4 Domain Adaptation Methods

域自适应方法使用来自源域的数据来提高学习模型在数据总是较少可用的不同目标域上的性能。由于源域和目标域之间通常存在不同的特征空间，为了更好地迁移源数据中的知识，我们应该尝试使这两个特征空间统一。这是域自适应的主要精神，可以用图3b中的图来描述。

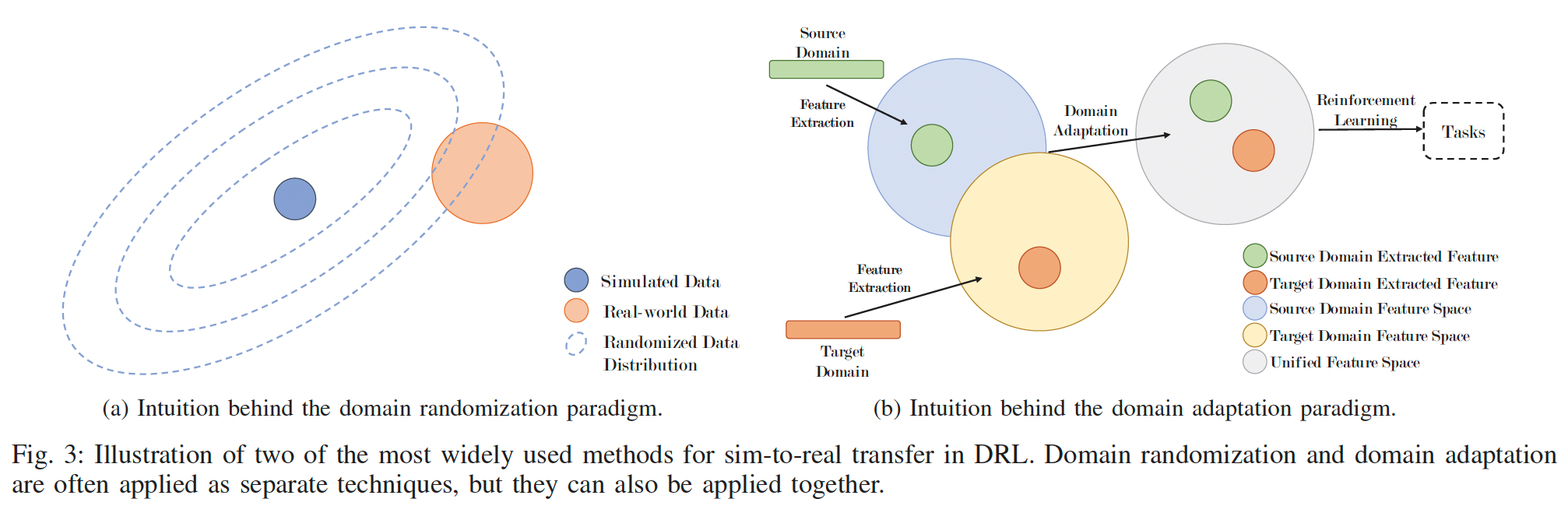
在此分类下，根据任务目的，还有下述两种分类，参考下文（但这篇文章不怎么样），这里参考了经典Robot policy learning的场景。

Dimitropoulos, K., Hatzilygeroudis, I., & Chatzilygeroudis, K. (2022). A brief survey of Sim2Real methods for robot learning. Advances in Service and Industrial Robotics: RAAD 2022, 133-140.

1. Randomizing for Perception：这类方法主要描述了“给定一个简单编程的控制器，创建可以推广到物理世界的感知模型”。这类方法的随机化对象主要是环境因素。

2. Randomizing for Control：这类方法主要目标是训练一个灵巧的控制主体，其随机化包括但不限于：关节位置、相机位置、随机干扰物、质量、滚动和旋转摩擦系数、光线、物体摆放位置等。

tax1.5 Learning with Disturbances (干扰)

Domain randomization 和 dynamics randomization侧重于在模拟环境中引入扰动，目的是使代理不易受模拟与现实之间不匹配的影响[30]、[38]、[40]。在其他作品中也扩展了相同的概念，其中引入了扰动以获得更鲁棒的代理。例如，在[72]中，作者考虑了嘈杂的奖励。虽然与模拟到真实的迁移没有直接关系，但嘈杂的奖励可以更好地模拟真实世界的代理训练。此外，在我们最近的一些作品中[8]，[73]，我们考虑了影响并行学习的不同代理的环境扰动。当要使用通用策略部署或训练多个真实代理时，这是需要考虑的一个方面。

tax1.6 Simulation Environments

sim2real的一个关键方面是模拟器的选择。独立于用于有效地将知识转移到真实机器人的技术，模拟器越逼真，预期的结果就越好。文献中使用最广泛的模拟器是 Gazebo [74]、Unity3D 和 PyBullet [75]或 MuJoCo [17]。Gazebo 具有与机器人操作系统 (ROS) 中间件广泛集成的优势，因此可以与真实机器人中存在的部分机器人堆栈一起使用。另一方面，PyBullet 和 MuJoCo 与 DL 和 RL 库以及体育馆环境进行了更广泛的集成。一般来说，Gazebo 适合更复杂的场景，而 PyBullet 和 MuJoCo 提供更快的训练。在以一次性传输的系统识别为目标的情况下，研究人员通常会构建或定制满足特定问题要求和约束的特定模拟[32]、[36]、[41]。

2. Domain randomization优化问题表述

Domain randomization问题可以表述为以下的双层优化问题

$$ \begin{array}{rl} \min & F(\phi, \theta) = \mathcal{L}(\theta^{*};\mathcal{D}_{real}) \\ \text{s.t.} & \theta^{*} = \arg\min_{\theta}f(\phi, \theta) = \mathbb{E}_{x \sim P_{\phi}(x)}[\mathcal{L}(\theta;\mathcal{D}_{x})]\\ \text{var.} & \phi, \theta \end{array} $$

• $\phi$：上层优化问题的变量，是一个控制生成随机化样本的分布的参数。

• $\theta$ ：下层优化问题的变量，是要学习的控制器、神经网络等具体模型的参数。

• $\mathcal{D}_{real}$ ：真实世界的数据集。

• $\mathcal{D}{x}$ ：合成数据集，生成该数据集的分布 $P{\phi}$ 受控于 $\phi$ 。

🌟 Franceschi, L., Frasconi, P., Salzo, S., Grazzi, R., & Pontil, M. (2018, July). Bilevel programming for hyperparameter optimization and meta-learning. In International Conference on Machine Learning (pp. 1568-1577). PMLR.

Marez, D., Borden, S., & Nans, L. (2020, May). UAV detection with a dataset augmented by domain randomization. In Geospatial Informatics X (Vol. 11398, pp. 39-50). SPIE.

以上表达是对DR问题的直接表达，即寻找一组恰当的仿真器参数，该参数与现实分布相似。但上述方法是一个non-convex non-smooth问题，其形式并不利于优化，目前解决这种优化问题的思路包括：

• 无需梯度的：贝叶斯优化、RL等无需求导运算的方法
• 基于梯度的：借助对抗思想，将原问题转化为单层的min-max问题

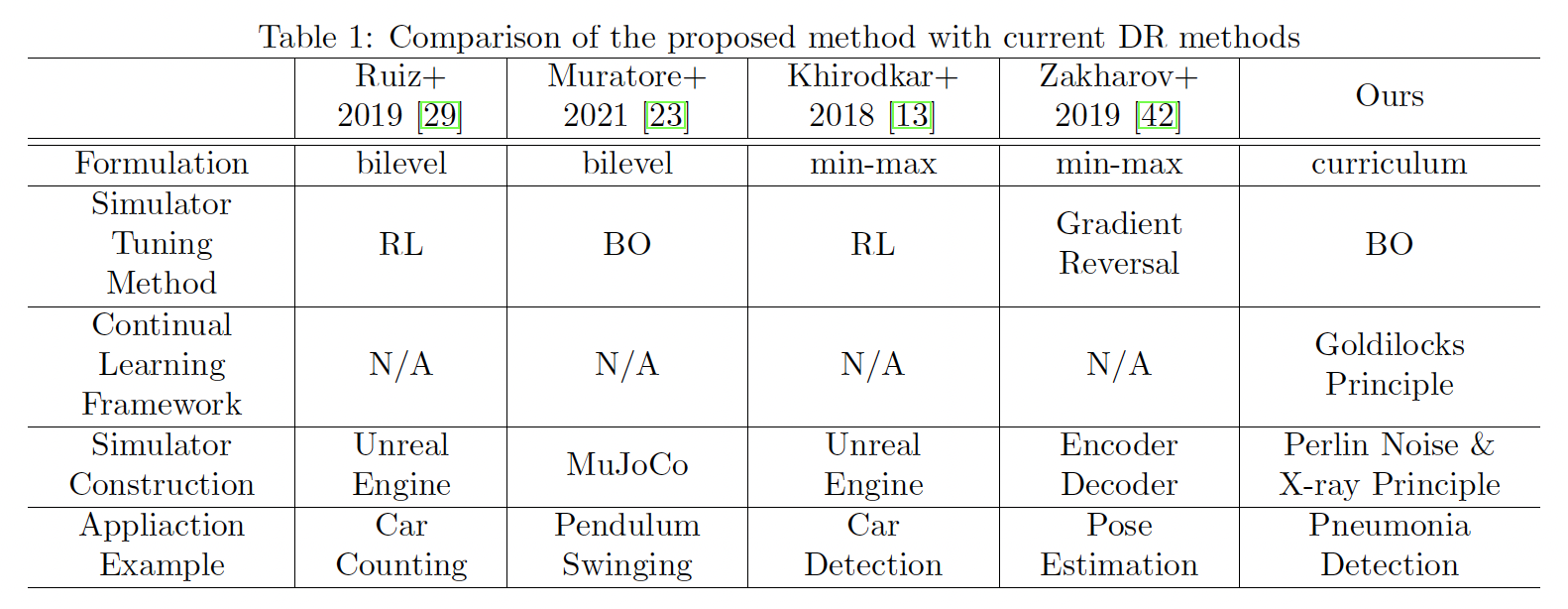
下图中是文献 “Goldilocks-curriculum Domain Randomization and Fractal Perlin Noise with Application to Sim2Real Pneumonia Lesion Detection” 中的方法总结。

3. 调研：基于Bi-level Optimization的DR问题求解

3.1 Gradient-free

1. 基于policy gradients (RL) 解双层优化问题（无代码）

Ruiz, N., Schulter, S., & Chandraker, M. Learning To Simulate. In 2019 International Conference on Learning Representations.

本文如第二节，将domain randomization问题表达为双层优化问题后，指出“基于梯度的方法是无法解该问题的（由于对内层问题的苛刻性质限制、数据生成函数受优化目标的影响、数据生成过程本身是不可微的）”，提出使用policy gradients解上述双层优化问题（见Sec. 2.2）。此外文章还讨论了simulator在实际场景下应该建模为一个Bayesian network或更复杂的网络，因为“actual data description (e.g., what objects are rendered in an image) is sampled from a distribution $S$ parametrized by the provided simulation parameters $\rho$ and specific rendering settings $\phi$ (e.g., lighting conditions) are sampled from a distribution $P$ also parameterized by $\psi$ , i.e. $G(x,y|\psi)=\mathcal{R}(S(\rho|\psi),P(\phi|\psi))$”

2. 用Bayes Optimization来解决外层优化问题，观察上述的formulation可以看出，外层优化问题是一个分布的优化问题，本工作用Gaussian Process来建模real world中代价函数，用贝叶斯法调整GP中的参数，以逼近真实世界的代价函数。**(Third party code available)**

Muratore, F., Eilers, C., Gienger, M., & Peters, J. (2021). Data-efficient domain randomization with bayesian optimization. IEEE Robotics and Automation Letters, 6(2), 911-918.

$$ \begin{aligned} \phi^{\star} & =\arg \max _{\phi \in \Phi} J^{\text {real }}\left(\theta^{\star}(\phi)\right) \quad \text { with } \\ \theta^{\star}(\phi) & =\arg \max _{\theta \in \Theta} \mathbb{E}_{\xi \sim \nu(\xi ; \phi)}[J(\theta, \xi)] \end{aligned} $$

其中外层优化问题用BO来解决，$\hat{J}^{real}(\theta^{\star}(\phi))$ 被建模为GP，The GPs’s mean and covariance is updated using all recorded inputs $\phi$ and the corresponding observations $\hat{J}^{real}(\theta^{\star}(\phi))$.

3. 本文提出，借助少量的真实世界数据，让RL算法从真实有效的分布开始，渐进、迭代式的学习更广、更宽的分布上的策略。

Y. Chebotar et al., “Closing the Sim-to-Real Loop: Adapting Simulation Randomization with Real World Experience,” 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 2019, pp. 8973-8979, doi: 10.1109/ICRA.2019.8793789.

本文的外层优化目标在上节的基础上细化为下式：

$$ \begin{array}{rl} \min _{\phi_{i+1}} & \mathbb{E}_{P_{\xi_{i+1} \sim p_{\phi_{i+1}}}}\left[\mathbb{E}_{\pi_{\theta, p_{\phi_i}}}\left[D\left(\tau_{\xi_{i+1}}^{o b}, \tau_{\text {real }}^{o b}\right)\right]\right] \\ \text { s.t. } & D_{K L}\left(p_{\phi_{i+1}} \| p_{\phi_i}\right) \leq \epsilon \end{array} $$

这里限制了simulator每次的变化程度。本文指出，$p_{\phi_0}$ 应当从一个真实有效的分布开始学起。对于上述外层优化目标，本文采用**relative entropy policy search**来解决，这是一种sampling-based、gradient-free的方法。

4. 基于Cross entropy method (CEM) 和proximal policy optimization (PPO)分别解决上述的外层和内层优化问题（dockerized code aviliable）

Vuong, Q., Vikram, S., Su, H., Gao, S., & Christensen, H. I. (2019). How to pick the domain randomization parameters for sim-to-real transfer of reinforcement learning policies?. arXiv preprint arXiv:1903.11774.

本文的内层优化问题是一个policy learning问题，本文的中心思想是借助少量优先的真实世界样本来矫正simulator。本文提出基于Cross entropy method (CEM) 和proximal policy optimization (PPO)分别解决上述的外层和内层优化问题，其中CEM作为解domain randomization问题的关键，是一种iterative gradient-free stochastic optimization method。

5. Active domain randomization (RL-based)：传统DR需要显式的给出一组随机参数、以及对应的取值空间，常用的经典做法是——在取值空间中做均匀采样，以生成不同类型的环境。但有工作证明，这样的均匀采样导致模型学习了过多不常出现的环境策略，从而导致低效学习。本文提出，将simulator变量取值空间中的变量生成问题也看作称一个RL问题，并使用学习算法来学习如何在空间中采样。该方法的外层优化目标也是一个RL问题。

Raparthy, S. C., Mehta, B., Golemo, F., & Paull, L. (2020). Generating automatic curricula via self-supervised active domain randomization. arXiv preprint arXiv:2002.07911.

3.2 Gradient-based

1. 引入对抗思想，将bilevel问题转化为单层的minmax问题

Zakharov, S., Kehl, W., Ilic, S.: Deceptionnet: Network-driven domain randomization. In: ICCV (2019)

2. 这篇没有找到原文，应该有更新的版本

Khirodkar, R., Yoo, D., Kitani, K.M.: VADRA: visual adversarial domain randomization and augmentation. CoRR abs/1812.00491 (2018)

3.3 others

1. 引入Goldilocks Principle：在curriculum learning的领域，以一种meaningful的order训练模型对模型学习策略是十分有效的，换言之，在学习过程中有一个学习任务的sweet point，在该点上持续学习，可以最大程度的提升模型性能（大概是这个意思，可能不准）。改工作的formulation不同于上一节。

Suzuki, T., Hanaoka, S., & Sato, I. (2022). Goldilocks-curriculum Domain Randomization and Fractal Perlin Noise with Application to Sim2Real Pneumonia Lesion Detection. arXiv preprint arXiv:2204.13849.

该工作的内外层优化目标分别为函数为

$$ \begin{array}{c} \phi^{t+1}=\arg \max_{\phi \in \Phi}-\left|V(\theta^t, S_\phi)-k\right| \\ \theta^t=\arg \min_{\theta} \sum_{i=1}^t L(\theta, S_{\phi^i}) \end{array} $$

内层：求训练一个分类器，该分类器在所有模拟器参数上的平均性能达到最优。外层：区别于其他工作，是一种curriculum-based method，它通过调整 $k$ 来获得对对给定的模型来说具有不同难度的任务，该方法试图找到一个sweet point，在该点上，模型可以最有效的进行学习（原文：Goldilocks principle suggests that there might be a **sweet spot** of task difficulty that **is effective to successfully progress the training** of the current model）。

4. 提及bilevel formulation但未给出解决方法的工作

还有一些文献没有提出具体的bilevel优化解决方法，但套用了该概念做了论文陈述，如:

[1] 仅说明了 $S \subseteq R $ 即：the feature space of synthetic dataset must encompass features from the real world data。

[1] Shamsuddin, A. F., Ragunathan, K., Abhijith, P., PM, D. R. S., & Sankaran, P. (2022). From synthetic to natural—single natural image dehazing deep networks using synthetic dataset domain randomization. Journal of Visual Communication and Image Representation, 89, 103636.